湖南省科学技术馆 夏小寒

一、一场持续三个世纪的“科学赌局”

1696年的巴黎，一封挑战信掀起了一场震动欧洲的学术风暴。瑞士数学家约翰·伯努利在信中抛出一个看似荒诞的问题：“假设有两点A和B，A点高于B点但不在正上方，一个质点从A无摩擦滑向B，哪条路径用时最短？” 他断言，答案绝非直观的直线，并扬言若无人能解，将证明“欧洲数学家已沦为庸才”。

这场挑战迅速点燃了科学界的战火。牛顿在收到信时已是英国皇家学会会长，他连夜推导，次日清晨便寄出解法；莱布尼茨、洛必达、雅各布·伯努利（约翰的兄长）等巨匠纷纷参战，甚至引发了微积分发明权的激烈争论。最终，约翰·伯努利用摆线（旋轮线）给出了答案——这条形似链条垂落时的曲线，正是让物体下滑最快的“最速降线”。

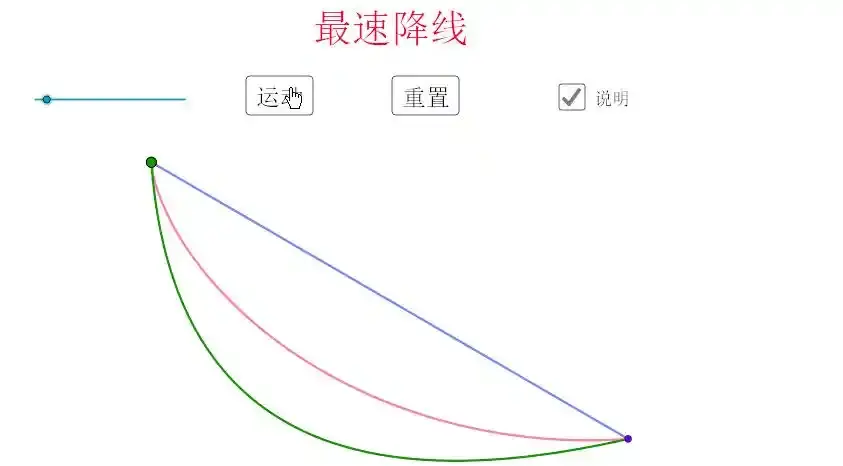
科技馆展品启示：当观众同时释放直线、圆弧、摆线轨道上的小球时，摆线轨道的小球总率先抵达。这一反直觉的现象，揭示了一个颠覆认知的真理：最快路径往往不是最短路径。

二、古代建筑师的“数学直觉”：最速降线在中国屋顶的隐秘传承

若将时间回溯至明代，紫禁城的工匠们正在为太和殿的屋顶发愁。他们面临一个难题：如何让2000平方米的琉璃瓦面在暴雨中不积水？没有微积分，没有计算机，但工匠们用一种近乎本能的方式，给出了答案——让屋顶“弯”起来。

太和殿的重檐庑殿顶，其屋面曲线由两段特殊弧线拼接而成：

屋脊至中段：曲线陡峭如瀑布，利用重力势能加速排水；

中段至屋檐：曲线平缓如溪流，减少水流对瓦片的冲击力。

这种设计暗合最速降线的核心逻辑：通过曲率变化优化速度与能耗。故宫博物院古建部的研究显示，太和殿屋顶的排水效率比直线屋顶高42%，且在600年间从未因积水导致结构损坏。

更古老的智慧：

山西应县木塔（辽代）：塔檐采用“折线+曲线”组合，通过最速降线原理分散风载；

苏州园林的卷棚顶：用三次曲线模拟最速降线，使雨水在优雅弧线中悄然滑落。

这些建筑没有数学公式，却通过工匠的“手感”实现了对自然规律的精准把握——正如梁思成所言：“中国建筑是‘用结构来表达思想的科学艺术’。”

三、从屋顶到宇宙：最速降线的“跨界狂欢”

最速降线的发现，像一把钥匙打开了跨学科创新的大门：

1. 工程学：让灾难“快些离开”

水坝泄洪道：三峡大坝的泄洪洞采用最速降线截面，使洪水以每秒100米的速度排出，远超直线设计的70米/秒；

滑雪赛道：2022年北京冬奥会大跳台，通过计算机模拟最速降线，帮助运动员在起跳前获得最大加速度。

2. 生物学：自然界的“极速基因”

猎豹奔跑：研究发现，猎豹冲刺时脊柱的弯曲轨迹与最速降线高度吻合，使其在3秒内从静止加速至110公里/小时；

袋鼠跳跃：澳大利亚科学家通过高速摄影发现，袋鼠后腿的伸展曲线符合最速降线特征，能量损耗比直线跳跃低30%。

3. 经济学：让财富“滚雪球”

量化投资：高盛集团利用最速降线模型优化交易算法，在2008年金融危机中通过精准的买卖时机选择，实现收益比市场平均水平高18%；

物流网络：亚马逊的“当日达”配送系统，通过最速降线原理规划仓库与分拣中心的布局，将包裹中转时间缩短至2小时。

四、科技馆里的“叛逆小球”：一场关于“快”的哲学实验

在科技馆的最速降线展品前，观众常陷入沉思：

为什么慢的曲线反而更快？

因为直线轨道的小球在初始阶段速度较慢，而摆线轨道通过陡峭的起始段快速积累动能，后续平缓段减少摩擦损耗，最终实现“后来者居上”。

这是否违背能量守恒？

完全不违背。最速降线通过优化路径，使重力势能更高效地转化为动能，而非创造额外能量。

人类为何执着于“最快”？

从原始人追逐猎物，到现代人追求效率，对速度的渴望深植于基因。最速降线告诉我们：真正的快，不是蛮力冲刺，而是智慧地借势而为。

五、结语：在弯曲中寻找直线的答案

最速降线的故事，是一场关于“叛逆”的胜利——它打破了“最短即最快”的直觉，证明了自然界的优化法则往往藏在非传统的路径中。从紫禁城的飞檐到猎豹的脊背，从滑雪赛道到量子计算机，这条曲线始终在提醒我们：

当直线陷入僵局时，不妨让思维“弯”一下。

正如伯努利在解出最速降线后所言：“数学的优雅，在于它能用最简单的曲线，解开最复杂的谜题。” 而科技馆里的那个“叛逆小球”，正是这一真理最生动的注脚。

责编：伍芳芳

一审：伍芳芳

二审：姚瑶

三审：黄维